Celý život se učíš!

Oblíbené odkazy

Navigace: Matematika 3.A > Vztahy mezi: Sin, Cos, Tg, Cotg

Vztahy mezi: Sin, Cos, Tg, Cotg

Vztah mezi sinem a cosinem

Goniometrické funkce mají mezi sebou blízké vztahy. Když se podíváte na graf funkce sinus a cosinus současně, tak zjistíte, že se od sebe moc neliší, že jedna je jen trochu posunutá oproti té druhé.

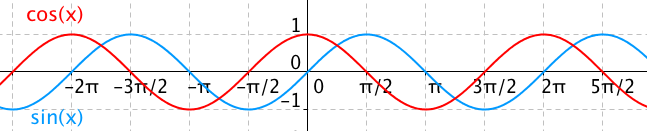Funkce sinus a cosinus jsou jen posunuté o π/2

Takže pokud k argumentu funkce vždy přičteme π/2, dostaneme funkci cosinus:

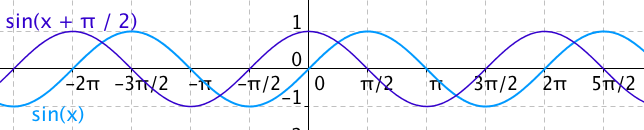Funkce sinus posunutá o π/2 — křivka je shodná s grafem funkce cosinus

A naopak, pokud u cosinu odečteme π/2, dostaneme sinus.

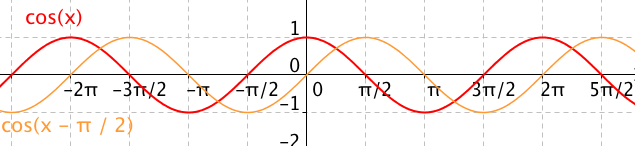Funkce cosinus posunutá o π/2 zpět — křivka je shodná s grafem funkce sinus

Můžeme tak napsat tyto vzorce:

$alt: \parstyle\begin{eqnarray*} \sin(x)&=&\cos(x-\frac{\pi}{2})\\ \cos(x)&=&\sin(x+\frac{\pi}{2}) \end{eqnarray*}$

Jak vyjádřit tangens a cotangens

Funkci tangens můžeme lehce vyjádřit pomocí sinu a cosinu. Stačí si uvědomit, co to tangens je: poměr délek protilehlé odvěsny ku délce přilehlé přeponě. Vezmeme si na pomoc tento trojúhelník:

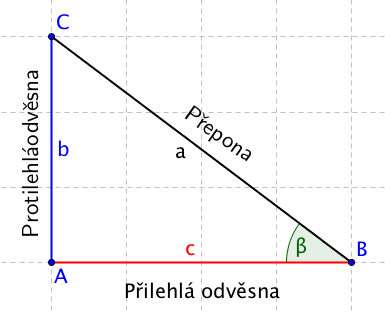Trojúhelní s vyznačeným úhlem beta

Čemu se rovná tangens úhlu beta?

$alt: \tan(\beta)=\frac{|b|}{|c|}.$

Jak bychom mohli vyjádřit čitatele nebo jmenovatele? Čemu se rovná délka stranyb a délka strany c? Víme, že sinus úhlu beta je roven:

$alt: \sin(\beta)=\frac{|b|}{|a|}$

Z toho vzorce osamostatníme |b|:

$alt: |b|=\sin(\beta)\cdot|a|$

Cosinus úhlu beta je rovný:

$alt: \cos(\beta)=\frac{|c|}{|a|}$

Osamostatníme |c|:

$alt: |c|=\cos(\beta)\cdot|a|$

V tuto chvíli máme délky stran b a c vyjádřené pomocí funkcí sinus cosinus. Dosadíme tak tyto mezivýsledky do původní rovnice s tangensem:

$alt: \tan(\beta)=\frac{|b|}{|c|}=\frac{\sin(\beta)\cdot|a|}{\cos(\beta)\cdot|a|}$

Z čitatele a jmenovatele můžeme zkrátit |a| a dostaneme konečný vzorec:

$alt: \tan(\beta)=\frac{\sin(\beta)}{\cos(\beta)}$

Tangens tak můžeme rozepsat jako podíl sinu a cosinu. Už bez odvození si povíme, že cotangens můžeme napsat jako obrácený zlomek, tj. podíl cosinus lomeno sinus.

$alt: \parstyle\begin{eqnarray*} \tan(\alpha)&=&\frac{\sin(\alpha)}{\cos(\alpha)}\\ \cot(\alpha)&=&\frac{\cos(\alpha)}{\sin(\alpha)} \end{eqnarray*}$

Vztah mezi tangensem a cotangensem

Podobně jako jsou si podobné funkce sinus a cosinus, jsou si podobné i funkce tangens a cotangens. Prohlédněte si oba grafy v jednom obrázku:

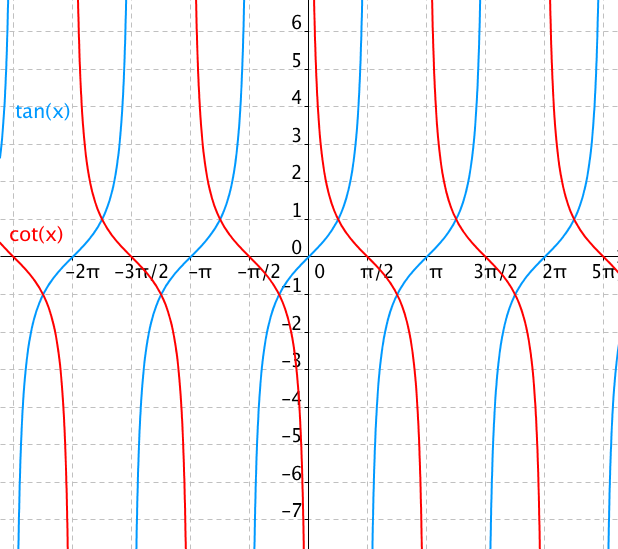Podobnost funkcí tangens a cotangens

Jakým způsobem uděláme z křivky, která popisuje tangens, křivku popisující cotangens? Cotangens je posunutý o π/2, tím začneme:

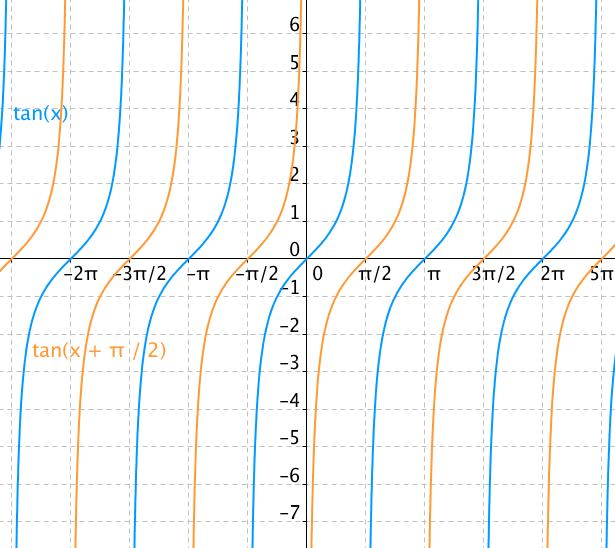Tangens posunutý o π/2

Už jsme se dostali blíže ke cotangensu, ale stále máme křivky ve špatné směru, cotangens je ve vybraných intervalech klesající, zatímco tato posunutá křivka je rostoucí. Tomu pomůžeme tak, že změníme znaménko proměnné x:

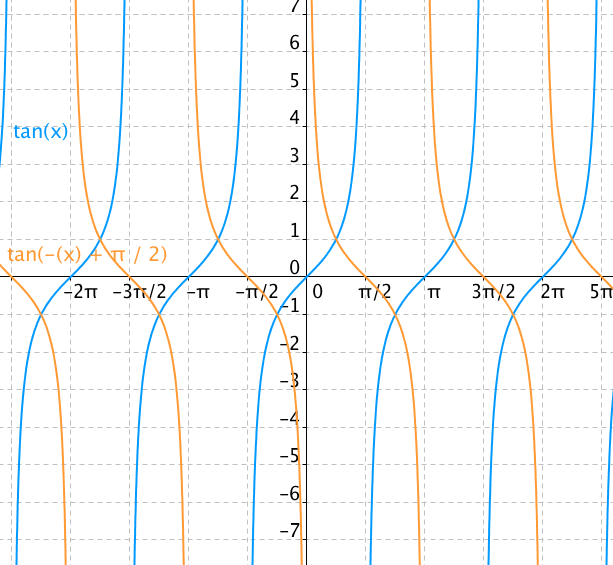Graf funkce tangens a cotangens

Můžeme tak napsat:

$alt: \cot(x)=\tan(-x+\frac{\pi}{2})$

Tabulkové hodnoty

Sinus, cosinus, tangens a cotangens mají pro některé hezké úhly hezké výsledné hodnoty. Zde je jejich základní přehled:

$alt: \LARGE \begin{matrix} &\sin&\cos&\tan&\cot\\ 0^\circ&0&1&0&\times\\ 30^\circ&\frac12&\frac{\sqrt{3}}{2}&\frac{\sqrt{3}}{3}&\sqrt{3}\\ 45^\circ&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}&1&1\\ 60^\circ&\frac{\sqrt{3}}{2}&\frac12&\sqrt{3}&\frac{\sqrt{3}}{3}\\ 90^\circ&1&0&\times&0 \end{matrix}$

Login:
Heslo:

Menu

Oblíbené odkazy

Vztahy mezi: Sin, Cos, Tg, Cotg